Boolean Expressions and Operators BEHIND THE SCENES!
Hi! Welcome to Boolean Expressions Behind the Scenes! :-)
On this occasion we will discuss Boolean Algebra, and how we can break down complex expressions into smaller components to determine what the whole expression ultimately evaluates to.
You will need Boolean algebra in many applications of computer science to determine certain “paths” or "alternatives" your code can follow during execution.
Example to be analyzed:
Let’s get started!
First of all, let’s dive in into what Boolean Algebra is at its core:
(As a curious fact, in Python’s shell you can operate on Truth Values (True and False) as if they were integers (1 and 0 respectively). Go ahead and try True + False or other variations of this example)
Our Boolean operators are and, or and not. Notice that the text is lowercase, even this first letter. This is because python is case sensitive and only recognizes these words as operators if they are completely lowercase
(You can try to use these operators in Python’s shell and you will see that it will throw an error if the keywords or, and or not are not lowercase).
Basic elements
But you may be thinking: Ok, these are operators, but what do they operate on? What do they connect? Well, they actually connect truth values (True and False). Let me explain myself:
- When we use a Boolean Operator “and” or “or”, the operator will be located between two Truth values (True or False) connecting them.
- When we use the operator “not”, there must be a truth value to its right.
On the image of Python’s Shell above, you can see two characteristics colors:
- The lines that start with >>> are expressions we gave as input.
- The words in yellow are keywords reserved in python so we can’t use them as variable names. They describe special values, operators and operations already predefined in python.
- The blue text that doesn’t have >>> is the value returned immediately after the line above with >>> was executed. E.g. False was returned when
True and Falsewas evaluated by Python.
Rules to analyze them
I’m sure you’re asking yourself where does this blue value come from? What are the rules or criteria to define if
True and False returns False?Truth Tables
A Boolean expression returns a Truth value according to a set of predefined rules called TRUTH TABLES:
Here you have the three truth tables we need to fully understand how expressions will be evaluated in Python.
p and q are expressions that will be evaluated to either True or False. E.g (5>6) is False and (3424242423>2) is True.
If we connect these expressions with the operators we’ve learned, these truth tables tell us what the final expression will evaluate to. In the diagrams there are more complicated expressions executed in the shell to demonstrate how each operator works and to prove that these rules are followed in Python.
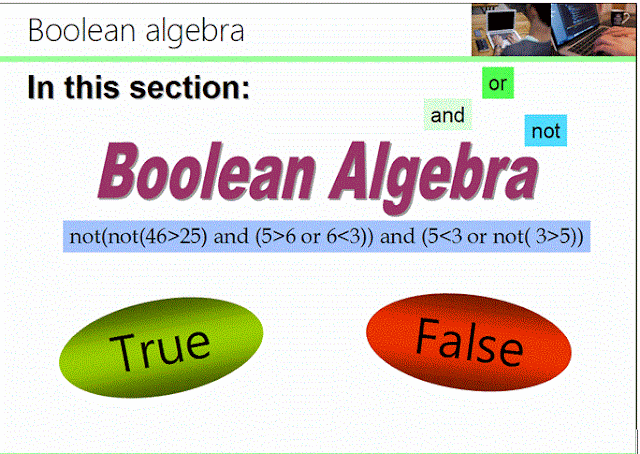
Breaking down an EXAMPLE into smaller components!
Now, let’s go to the actual example!
- First of all, you have to find the innermost level in the expression. This could be parenthesis or could be defined by operator precedence from left to right (check the course finger exercises for operators precedence).
- In this case, we start with the innermost parenthesis.
- STEP 1: When we find these parenthesis, we must convert the expressions connected by the operators to actual Truth values (True or False)
- STEP 2: Next, we can replace the previous small expressions with the Truth Value they evaluated to, so we can simplify the expression without altering the final result.
- You can notice that the last “not” operator is executed on this step. This is because it is located in the innermost level on this step and because of operator precedence. When you have two expressions connected by the or operator and one of the expressions if preceded by a not operator, the not operator is evaluated first.
- STEP 3: Again, we evaluate the innermost parenthesis
- STEP 4: We evaluate the not operator
- STEP 5: We evaluate the and operator
- Finally, we obtain a single Truth value. In this case is
Truebut it could beFalsefor other expressions.
You can check that this is correct by executing it on Python’s shell step by step or by giving the whole expression as an input and obtaining the final Boolean True (presented in the slide).
If you have any questions, please post them on the forums or right below this post.
Community TAs and your classmates are always there to help you on the forums! : )
COPYRIGHT= Concepts and truth tables were taken from Wikipedia articles
Hope it helps!
Thank you so much for your kind words.
Estefania.









Comments
Post a Comment