Python Numeral Systems (Decimal, Binary, Octal, Hexadecimal): Behind the Scenes

By

📌 Welcome to… Python Numeral Systems!👋

Welcome to this new tutorial. This time, you will learn about a very interesting aspect of Python, how you can work with numbers in different numeral systems (decimal, binary, octal, and hexadecimal).
Let’s begin! 😀
image

✨ Intro to Numeral Systems

Typically, when you work with numbers in Python, you use the decimal number system. For example, when you enter the number 1101 in the interactive shell, you see this:
>>> 1101
1101
The same number is returned because the “default” numeral system in Python is the decimal numeral system (base 10).
Note: the base of a numeral system is a key concept. The decimal numeral system has base 10 because it represents numbers using 10 digits (0-9) The resulting number is obtained by multiplying the digit by 10 raised to its corresponding power, moving from 0 for the rightmost element and increasing by one as we move to the left, as you can see in the following diagram:
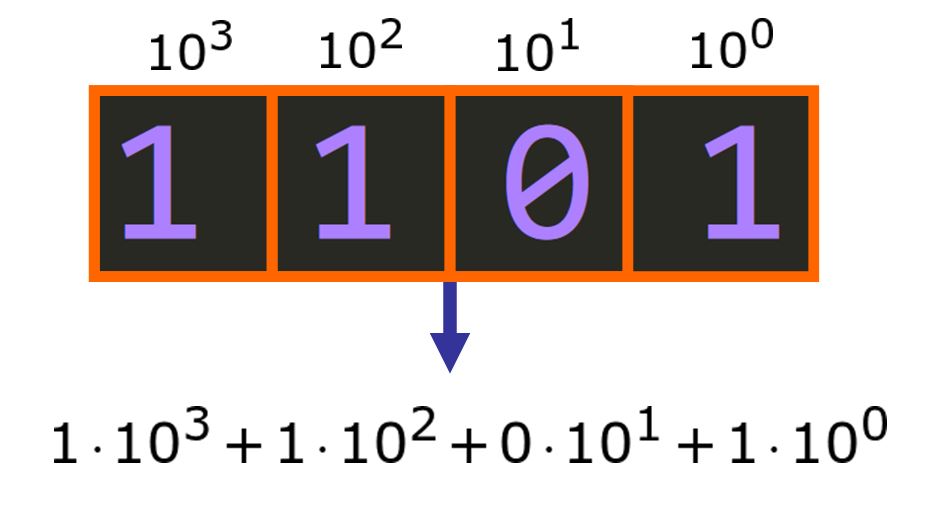
image
That expression results in 1101, the number that we are familiar with in the decimal system.

✨ Binary Numeral System

Now… what if we need to work with a binary number (base 2)? Only using 0s and 1s directly in Python will not work automatically because Python will not know that we want the number to be a binary number. The number will still be interpreted as a decimal number. 😱
We need to add a prefix to tell Python that we want to use a different numeral system.
The prefix to define a binary number in Python is 0b or 0B (they are equivalent).
Please see the structure of the binary number below. We have a prefix 0b followed by the binary number.
💡 Note: Once you add a prefix to specify a numeral system, you can only use digits that are valid in that numeral system. For example, you can only use 0s and 1s in the binary numeral system.
image
Now, if we enter this number in the interactive Shell, we see 13 displayed as the result. This is because Python automatically converts the binary number to a decimal number. To do this, you can multiply each digit by its corresponding factor:
1*(2^3) + 1 * (2^2) + 0 * (2^1) + 1*(2^0) = 13

✨ Octal Numeral System

Similarly, we have a special prefix to use numbers in the Octal Numeral System (base 8). The prefix is 0o or 0O.
Notice (in the diagram below) how the equivalent number in the decimal system is 3001, the result of multiplying each digit by its corresponding factor:
5 * (8^3) + 6 * (8^2) + 7 * (8^1) + 1 * (8 ^ 0) = 3001
image

✨ Hexadecimal Numeral System

The prefix used to write a number in the Hexadecimal Numeral System is 0x or 0X. In this numeral system, we have 16 digits, including the numbers 0-9 and letters “A” through “F”.
In this example (below), the result is 9345 in the decimal system after evaluating 2*(16^3) + 4*(16^2) + 8*(16^1) + 1*(16^0) to convert the number to the decimal numeral system.
image

⭐️ We can operate with them ⭐️

Interestingly, we can operate with numbers in different numeral systems. The result is a number in the decimal numeral system.
image

⭐️ We can convert numbers to a different numeral system⭐️

Python includes three built-in functions to convert a number from one numeral system to another:
For example:
>>> bin(56)          # Decimal to Binary
'0b111000'

>>> bin(0x5234)      # Hexadecimal to Binary
'0b101001000110100'

>>> bin(0o742)       # Octal to Binary
'0b111100010'
For example:
>>> oct(722)        # Decimal to Octal
'0o1322'

>>> oct(0b11011)    # Binary to Octal
'0o33'

>>> oct(0x1273)     # Hexadecimal to Octal
'0o11163'
For example:
>>> hex(632)        # Decimal to Hexadecimal
'0x278'

>>> hex(0b110111)   # Binary to Hexadecimal
'0x37'

>>> hex(0o1536)     # Octal to Hexadecimal
'0x35e'
I really hope that you liked this tutorial and found it helpful. 😀 Please do not hesitate to ask on the discussion forums or right below this post if you have any questions. Community TAs and your classmates will always be there to help you.
Estefania.

Comments

Post a Comment